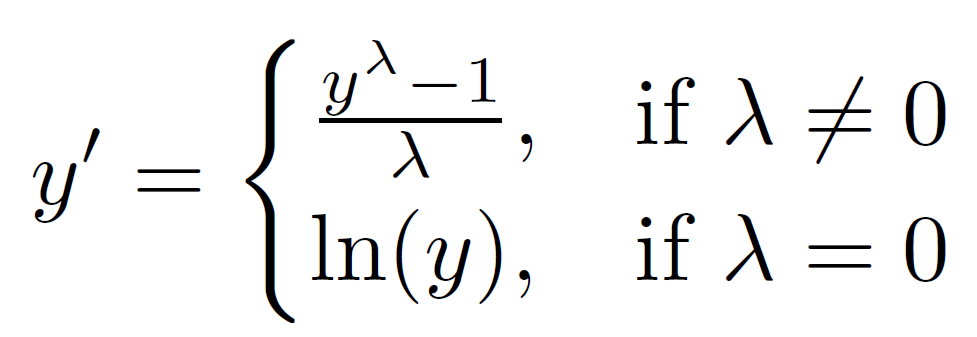多変量解析において、目的変数と説明変数の関係を適切に分析するためには、特徴量エンジニアリングが重要です。例えば、整数型の特徴量を扱う場合、単純に線形関係として扱う、非線形変換を適用する、ダミー変数化するなどの方法が考えられます。整数に対してそのまま線形回帰を適用すると、説明変数と目的変数の非線形な関係を適切に表現できない課題が残ります。

　本記事では、整数の連続変数の処理方法として、(1) そのまま使う、(2) Box-Cox変換を適用する、(3) ダミー変数化する、の3つの方法で、実際のデータを用いて各手法における説明変数と目的変数の関係の曲線を比較し、その特徴を分析します。

1. 検証の方法

　分析に用いるデータは、当社事業に関連するデータで、データサイズは約8万件です。

　こちらのデータを用いて重回帰分析を行う中で、範囲が0～60の整数型の特徴量に着目し、モデルの回帰曲線グラフを作成します。なお、今回は対象とする整数以外にも約10項目程度の説明変数を付けて計算しています。

2-1. 変数をそのまま利用した場合

特徴量エンジニアリングを行わず、そのまま重回帰分析を行った場合の回帰曲線（直線）は以下のようになりました。

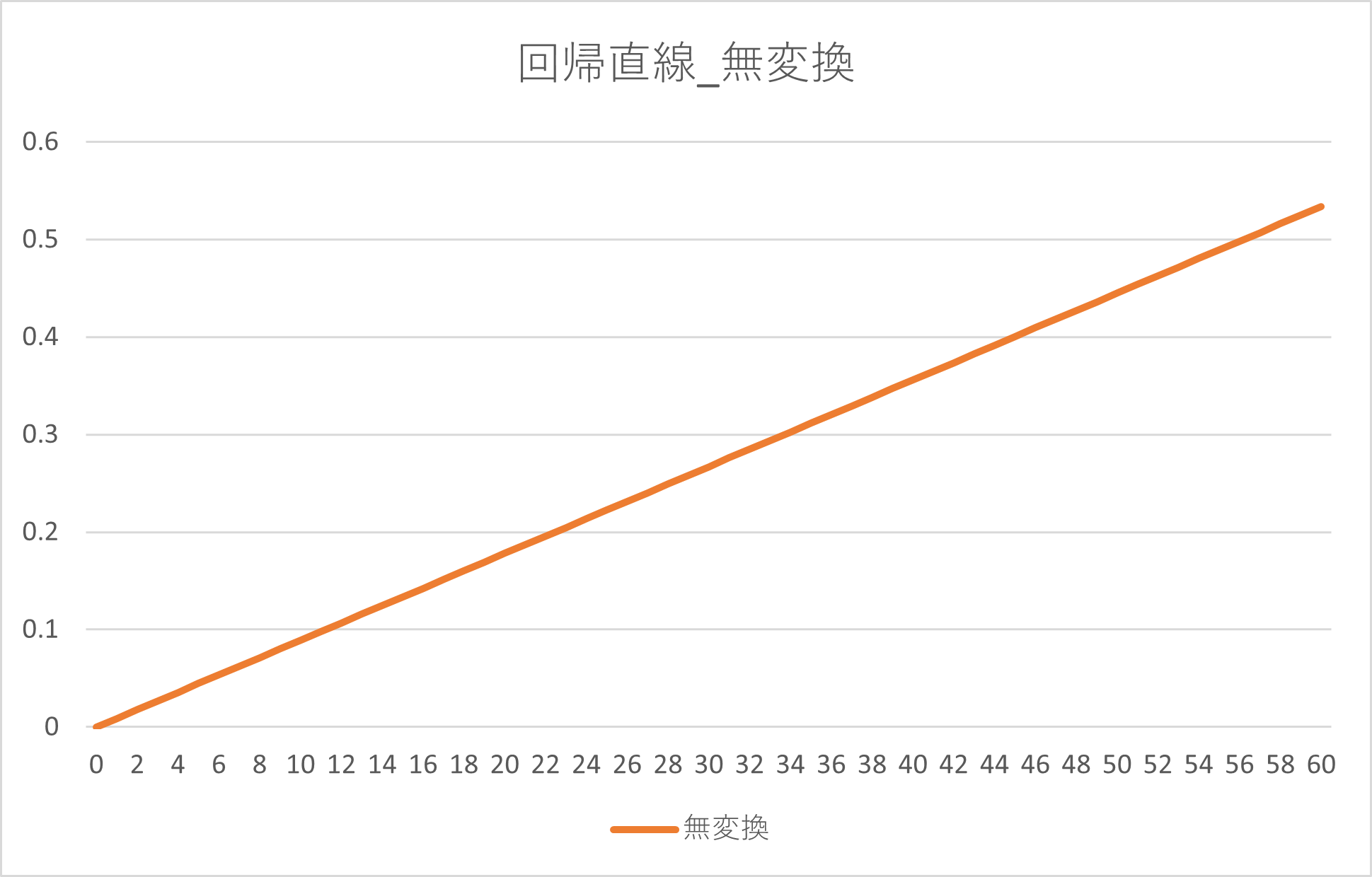
シンプルな直線でわかりやすいのが特徴です。

2-2. Box-Cox変換を行った場合

　次に、Box-Cox変換変換を行って回帰曲線を算出します。Box-Cox変換は、データの分布を正規分布に近づけるための変換手法であり、最適なパラメータλを求めた上で、以下の式を使って変数の変換を行います。

　なお、Box-Cox変換は0を含む整数データには直接適用できない方法のため、今回は全ての値に1を加えて適用しました。

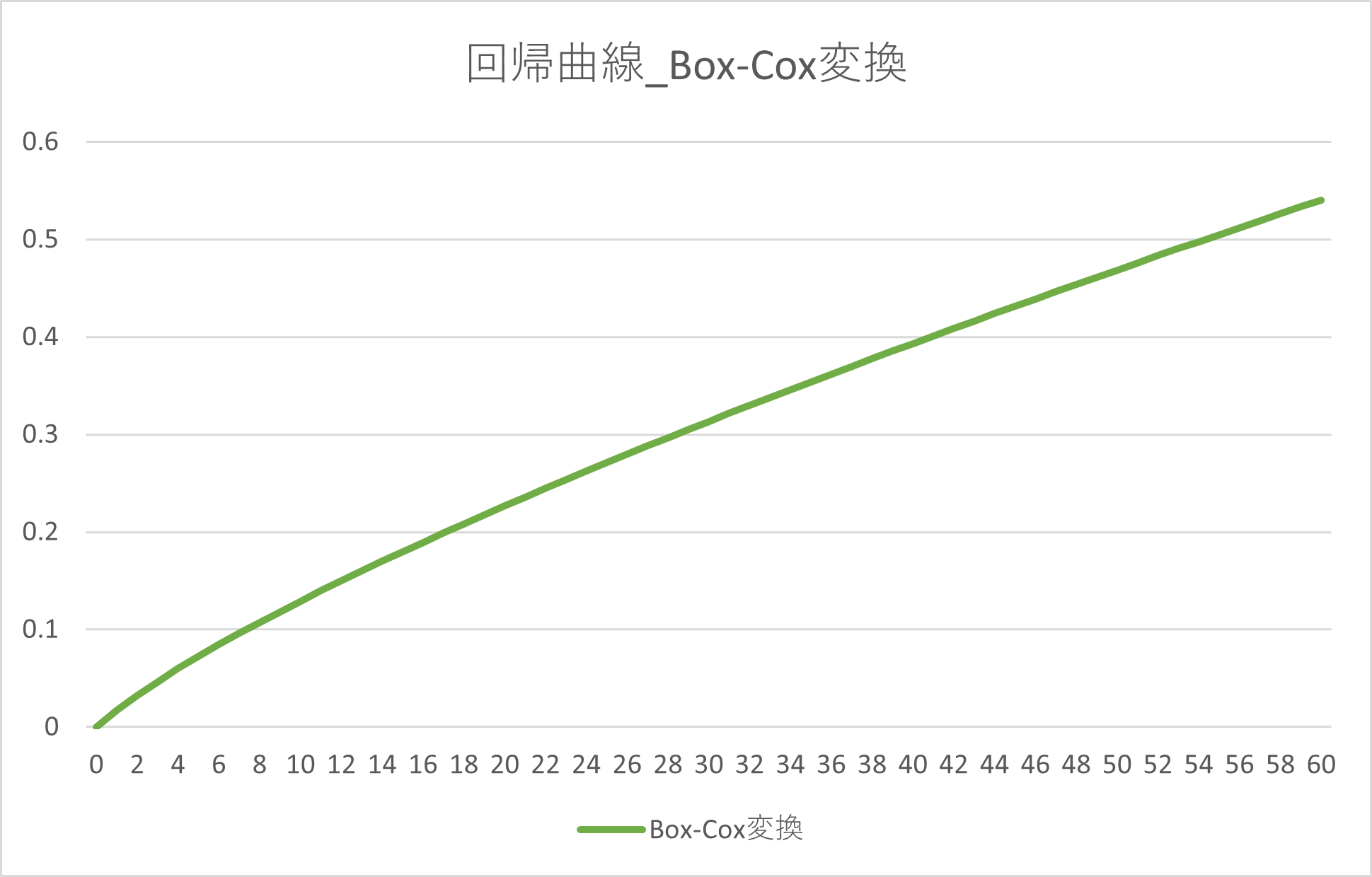
　Box-Cox変換による説明変数の非線形変換を行った上で重回帰分析を行い、値を元の説明変数に戻して回帰曲線グラフを作成したところ以下のようになりました。

　先ほどは直線だった回帰曲線が曲線になり、小さい値でより変化率が大きいことがわかります。

2-3. ダミー変数化を行った場合

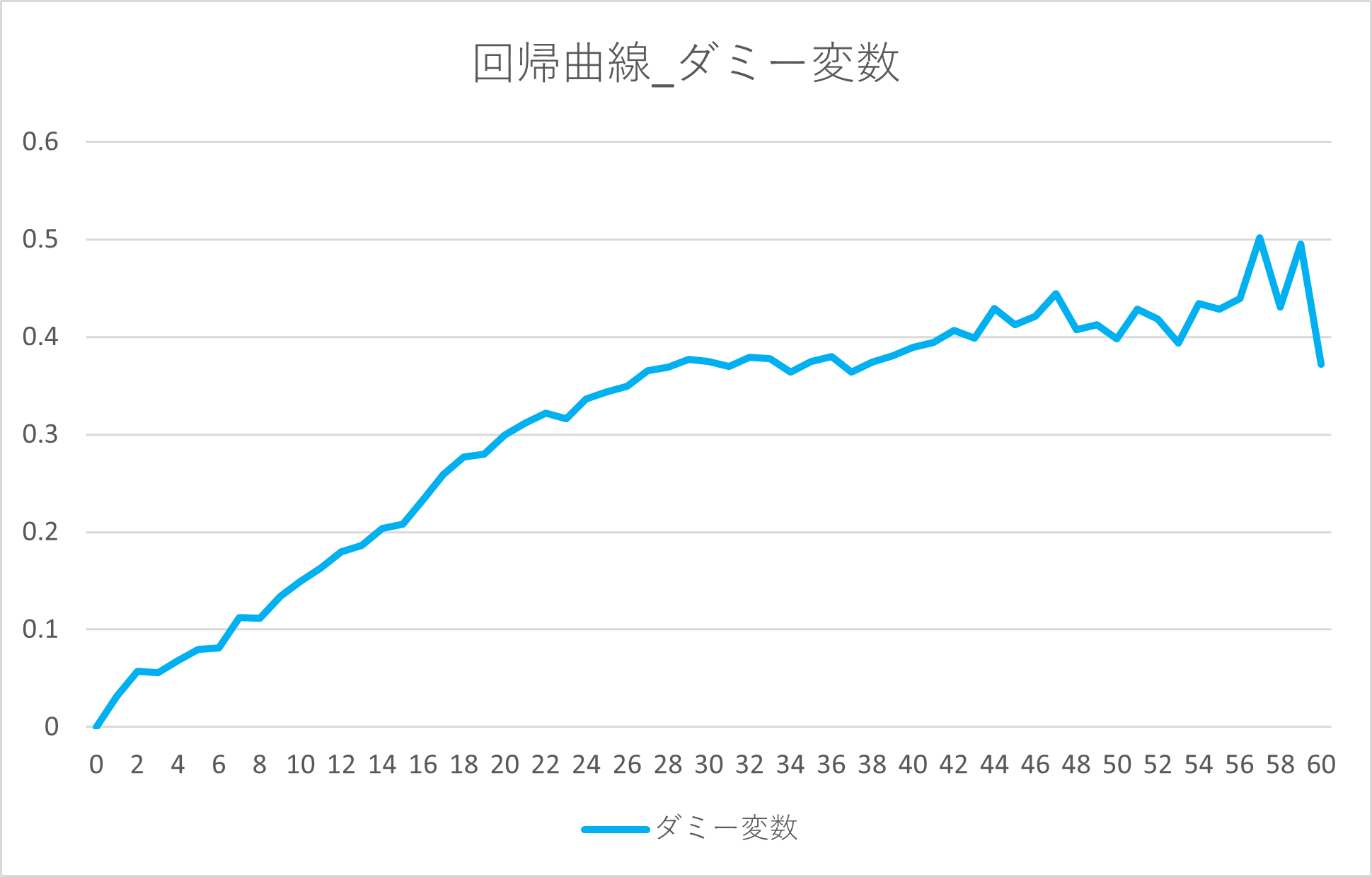
　最後に、0から60までの整数を全てダミー変数化し、それぞれのダミー変数への係数を用いて作成した回帰曲線は以下のようになりました。

　今回は単純に全ての値をダミー変数化しましたが、0から60までの整数をそのままダミー変数化すると、次元が増えすぎて過学習しやすくなるため、一定の間隔でグループ化するなども有効です。

　全体的な傾向として、しばらく一定の変化率で推移した後、途中からは数値の上昇に伴う変化が小さくなっています。ただし、全体的に曲線が不安定であり、特に対象となるデータが少ない60近くでは激しく値がばらついてしまっています。現実的に利用するためには、さらにこの回帰曲線を近似するなどの工夫が必要そうです。

3. まとめ

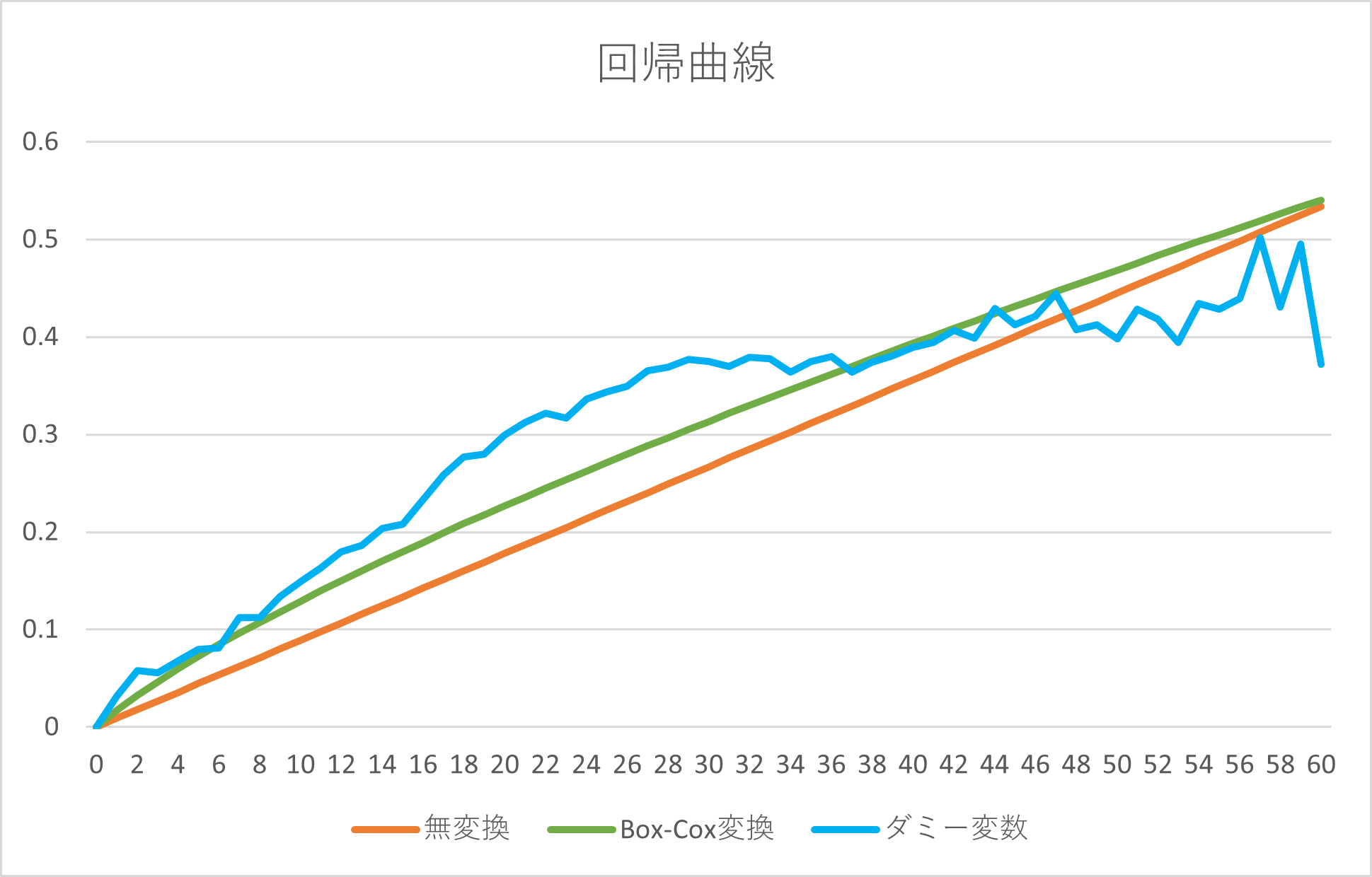
3つの回帰曲線を1枚のグラフにまとめると以下のようになります。

　特徴量エンジニアリング以外は全て同じ条件で計算しましたが、異なる回帰曲線が示されています。ダミー変数の結果からは、目的変数と説明変数の関係性としては説明変数が小さい場合により顕著に変化する可能性がありますが、連続変数をそのまま使うとその関係性がうまく表現できていません。一方、ダミー変数化による回帰曲線はノイズを含み不安定になりやすく、また、データが十分にない場合はそもそもダミー変数化することも難しくなります。

　他にも、説明変数を2乗したパラメータを追加するなど、様々な特徴量エンジニアリングが考えられます。ただし、それぞれの方法に特徴があるため、利用するデータの特徴の理解やドメイン知識の活用によって、適切なモデルを選択する必要が求められるでしょう。