はじめに

「シフト表作成問題」、通称「ナーススケジューリング問題」は、スタッフ一人ひとりの希望や労働規則といった多様な条件を考慮しながら、各日・各シフトに適切な人員を配置する数理最適化問題です。複数の制約（各日の必要人数、連続勤務の制限、休暇要件など）を満たしつつ、スタッフの満足度向上や人件費の最適化といった目的を達成することを目指します。

数理モデルとしては、どのスタッフがいつどのシフトに入るかを「0」か「1」で表現する0-1変数を使い、様々な制約条件下で目的関数の最適化を行う整数計画問題として定式化するのが一般的です。

この記事では、シフト表作成でよく登場する代表的な条件と、それらを数式で表現する定式化の具体例を紹介します。

シフト表作成における「よくある条件」

まずは、多くのシフト表で考慮される基本的な条件を4つ見ていきましょう。

1. 休みの希望

個人的な予定（冠婚葬祭や子の学校行事など）のために、特定の日に休みを取りたいという要望です。スタッフの満足度や働きがいに直結するため、非常に重要な条件として扱われます。

2. 休みの回数

労働関連法規や就業規則で定められた、月間の最低休日数に関する条件です。例えば「月に8日以上の休みを確保する」といったルールがこれにあたります。スタッフの健康を守り、過重労働を防ぐための必須制約です。

3. 各シフトの必要人数

「日勤は5人以上」「夜勤は2人以上」のように、各シフト（早番・日勤・遅番・夜勤など）で必要となる最小人数を定めた条件です。医療やサービスの質と安全性を担保するための根幹となる制約です。

4. 特定の勤務の禁止（夜勤明けなど）

十分な休息時間を確保するため、夜勤の翌日に早番や日勤といった負担の大きい勤務を割り当てない、というルールです。スタッフの健康と、それによって保たれる医療安全の観点から重要な制約となります。

数理モデルによる定式化

それでは、これらの条件を数式でどのように表現するのかを見ていきましょう。

基本的な変数の定義

この問題を数式で表現するために、まずは基本となる集合と、0-1決定変数を以下のように定義します。

各種制約の定式化

次に、先ほど説明した4つの「よくある条件」を、定義した変数を使って数式で表現します。

モデルの前提となる基本制約

上記の制約が正しく機能するためには、モデル全体の大前提となる以下の基本制約が必要です。

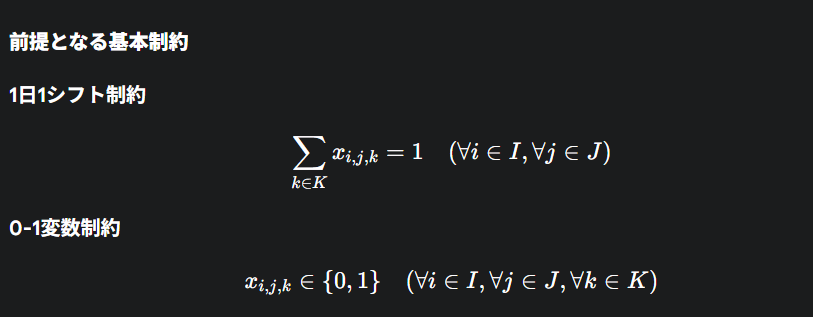
まとめ

このように、シフト表作成における一般的な制約条件は、0-1整数計画問題として明確に定式化できます。実際の現場では、ここで紹介した基本制約に加えて、さらに複雑な条件が求められることも多いですが、その場合も同様のアプローチで数式に落とし込むことが可能です。

実は、今回紹介した条件をさらに抽象化・一般化することで、現場で登場するほぼ全ての条件をカバーする万能なモデルを構築することもできます。本記事では、その土台となる「よくある条件」に焦点を当てて解説しました。

ザイマックスではシフト制の働き方の部署や部門ではシフト作成を整数計画問題として扱い、より働きやすいシフト作成作りに活用しています。